Происхожденіе нашихъ цифръ

Происхожденіе нашихъ цифръ

Т? цифры, которыя употребляются въ настоящее время почти вс?ми образованными народами и которыми пользуемся также и мы, называются обыкновенно арабскими; но это названіе он? получили вовсе не потому, что обязаны своимъ происхожденіемъ арабамъ: арабы ихъ только принесли въ Евроиу, а начало имъ дали, по всей в?роятности, индусы.

Д?йствительныя, подлинныя арабскія цифры не им?ютъ никакого отношенія къ нашимъ, которыми мы пользуемся теперь. Прежде всего надо сказать, что первоначальное письмо арабовъ было грубо и некрасиво, и едва ли до VII в. по Р. X. были у нихъ какія-нибудь цифры. Только со временъ Магомета, когда сразу былъ данъ чрезвычайный толчекъ развитію арабскаго могущества и образованности, стало у нихъ процв?тать и письмо. Арабы особенно любили выражать числа такъ, чтобы писать полныя числительныя имена; отсюда естественно вытекаетъ, что съ теченіемъ времени они перешли къ первымъ буквамъ числительныхъ именъ; впосл?дствіи, подобно грекамъ, они стали прим?нять буквы въ алфавитномъ порядк?.

Около 773 года по Р. X. арабы приняли индусскую систему цифръ и стали обозначать числа такъ, какъ ихъ обозначали индусы. Сд?лать это было т?мъ бол?е легко и естественно, что Индія граничила съ влад?ніями арабскихъ халифовъ, и между сос?дями постоянно были близкія сношенія и торговыя, и научныя.

Заслуга индусовъ въ развитіи ари?метики громадна и неисчислима. Во-первыхъ, они сильно уменьшили количество цифръ и довели его до 10, считая въ томъ числ? и нуль; между т?мъ, у грековъ, у евреевъ, у сирійцевъ и т. д. цифръ было не мен?е 27; правда, римляне ум?ли обходиться 7-ю цифрами, но за то у нихъ была маса мелкихъ значковъ, которые только спутывали и м?шали. Во-вторыхъ въ индусской систем? ясно проглядываетъ необыкновенная простота, точность и объединенность: каждый разрядъ выражается обязательноі одной цифрой, а не н?сколькими; значеніе цифры легко угадать по м?сту, которое она занимаетъ, и не надо задумываться ни надъ сложеніемъ, ни надъ вычитаніемъ сос?днихъ знаковъ, какъ это бываетъ въ другихъ системахъ; кром? того, десятки, сотни, тысячи и милліоны и высшіе разряды пишутся точно такъ же, какъ простыя единицы, поэтому не надо изобр?тать особенныхъ правилъ для высшихъ разрядовъ, а можно безконечно прилагать одно и то-же правило. Вс? эти выгоды настолько ясны и безспорны, что всякій народъ, какъ только ознакомится со способомъ индусовъ и пойметъ его, то перем?няетъ свою систему на ихъ систему. Такъ было и съ арабами, и съ Западной Европой, и съ нами русскими.

Главное преимущество индусской системы заключается въ томъ, что значеніе каждой цифры вполн? опред?ляется ея м?стомъ, т.-е. если, наприм., цифра стоитъ на 4-мъ м?ст? справа, то она выражаетъ тысячи, и, сл?д., чтобы написать тысячу, надо только поставить цифру 1 на 4-е м?сто, но не перем?нять ея формы и не припиеывать какого-нибудь особеннаго слова или значка. Въ глубокой древности встр?чались и среди иныхъ народовъ геніальные умы, которые какъ-то смутно догадывались, что значеніе цифры лучше всего опред?ляетсяется м?стомъ, но вс? они становились въ тупикъ передъ такимъ сомн?ніемъ: а какъ же быть, если какой-нибудь разрядъ въ числ? пропущенъ, напр., если число состоитъ только изъ единицъ и сотенъ и не содержитъ десятковъ? Ч?мъ зам?щать недостающіе разряды? Индусы отв?чали коротко и ясно: надо зам?щать нулемъ. И мы теперь, когда отв?тъ изв?стенъ, пожалуй, удивляемся, чего тутъ труднаго, и какъ же было не смекнуть; но жизнь доказываетъ лучше всякихъ словъ, что самыя простыя и общія идеи всегда и самыя мудреныя. Вотъ что говоритъ относительно этого изв?стный французскій математикъ Лапласъ:

«Мысль выражать вс? числа 9-ю знаками, придавая имъ, кром? значенія по форм?, еще значеніе по м?сту, настолько проста, что именно изъ-за этой простоты трудно понять, насколько она удивительна. Какъ нелегко было прійти къ этой метод?—мы видимъ ясно на прим?р? величайшихъ геніевъ греческой учености, Архимеда и Аполлонія, для которыхъ эта мысль осталась скрытой».

Вс? величайшія открытія никогда не являются вдругъ и сразу, наоборотъ для нихъ необходима продолжительная подготовка. Какъ же могли индусы прійти къ иде? обозначенія чиселъ? какъ они придумали нуль? В?рн?е всего посл? счета нагляднаго, т.-е. счета на пальцахъ, камешкахъ и черточкахъ они перешли къ спеціальнымъ счетнымъ приборамъ, именно къ шарикамъ и косточкамъ на проволокахъ и шнурахъ; зат?мъ естественно было чертить колонны на песк?, дощечкахъ и бумаг? и въ эти колонки или желобки класть т? же косточки и шарики. Дальн?йшая ступень: въ колоннахъ чертятся значки или кладутся въ нихъ костяшки съ награвированными цифрами; теперь остался одинъ шагъ и до того, чтобъ цифрамъ придавать значеніе по м?сту; д?йствительно, если вс? колонны заняты, то ихъ края, пожалуй, можно и стереть, потому что и безъ нихъ можно догадаться, что первая справа костяішка обозначаетъ единицы, сос?дняя, т.-е. вторая, десятки и т. д. Получится гладкая, ровная поверхность, на которой подрядъ лежатъ костяшки, или начерчены значки; но какъ же быть съ той колонной, въ которой н?тъ значка, потому что въ данномъ числ? н?тъ соотв?тствующихъ единицъ? Подобную колонну стирать нельзя, потому что иначе смыслъ вс?хъ другихъ, лежащихъ вл?во, изм?нится, но ее-то одну именно и достаточно начертить, положимъ въ такой форм?: || или II или 0. Сл?довательно, нуль образовался изъ фигуры пустой колонны.

Вотъ тотъ нормальный путь, которымъ можно постепенно отъ счета на предметахъ придти къ нулю. Путь этотъ очень продолжителенъ. Нужны тьсячел?тія, чтобы отъ пальцевъ перейти къ счетнымъ приборамъ, и отъ нихъ къ письму.

Цифры индусовъ произошли, нав?рное, отъ первыхъ буквъ числительныхъ именъ; это т?мъ бол?е возможно, что 9 первыхъ числительныхъ именъ въ ихъ язык? (въ санскритскомъ язык?) вс? начинаются съ различныхъ буквъ. Индусская система разстановки цифръ отъ правой руки къ л?вой по разрядамъ ведетъ начало съ III ст. по Р. X. Арабы ее переняли въ VIII стол?тіи и принесли въ Европу въ IX в?к?, но до XIII в?ка она распространялась въ христіанскихъ государствахъ очень слабо, потому что сначала, какъ и все новое, была встр?чена съ недов?ріемъ и съ трудомъ проникала въ народную массу. Нулемъ индусы стали пользоваться гораздо позже, около VІІ-го или VШ-го в?ка по Р. X. и во всякомъ случа? не ран?е V-го. Опред?ленное изв?стіе о нул? мы встр?чаемъ въ первый разъ въ 738 г. по Р. X.

Наши цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 получили, какъ признаетъ болынинство ученыхъ, начало отъ индусовъ, но это вовсе не значитъ, что цифры индусовъ им?ли именно такой видъ, какой он? им?ютъ у насъ.

Въ теченіе в?ковъ, переходя отъ народа къ народу и отъ ученаго къ ученому, изм?няясъ подъ вліяніемъ практики и удобства, он? усп?ли почти совершенно потерять свою прежнюю форму и вылиться въ новую, непохожую; отъ старинныхъ первоначальныхъ индусскихъ цифръ остались только слабые намеки въ цифрахъ 1, 5, 8, да и то посл?дняя цифра писалась въ горизонтальномъ положенiи, вм?сто вертикальнаго; но во всякомъ случа? совершенно возиожно просл?дить, какъ изъ первоначальныхъ фигуръ постепенно получились дальн?йшія; и вотъ эта-то возможность просл?дить и доказываетъ намъ, что цифры получили начало у индусовъ. Въ XIII стол?тіи, когда индусская система сд?лалась изв?стной вс?мъ европейскимъ математикамъ, мы видимъ 1, 3, 6, 8, 9, 0 въ той самой форм?, въ какой он? употребляются и теперь, а остальныя четыре цифры не похожи на наши нын?шнія. Въ XV стол?тіи окончательно выработались цифры 2 и 4, но 7 упорно продолжало писаться въ вид? ижицы или угла. 5 дольше вс?хъ не получало нын?шняго своего облика и продолжало изображаться схоже съ 4-мя. Едва въ XVI стол?тіи можно въ первый разъ встр?тить систему 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 въ ея нын?шнемъ, вс?мъ намъ изв?стномъ вид?. Всю эту изм?нчивость цифръ легко объяснить т?мъ, что до 1471 года, когда было отпечатано въ первый разъ математическое сочиненіе типографскимъ шрифтомъ, вс? книги переписывались ручнымъ способомъ, и вліяніе переписчиковъ на изм?неніе формъ цифръ могло быть громаднымъ. Кром? того, надо принять во вниманіе, что развитіе цифровыхъ фигуръ шло въ теченіе многихъ сотенъ л?тъ, и въ немъ принимали участіе почти вс? образованные народы того времени. И если въ наши дни, когда образованіе достигло высокой степени объединенія, когда печатные шрифты получили устойчивую форму, все-таки зам?чается разнообразіе въ печатныхъ буквахъ и въ различныхъ почеркахъ, то, т?мъ бол?е оно должно было проявляться въ средніе в?ка, когда произволу переписчиковъ открывалась широкая возможность. (Образцы различныхъ типовъ цифръ мы пом?щаемъ въ приложеніи 10-мъ въ конц? книги).

Итакъ, мы изложили, какъ постепенно изъ индусскихъ цифръ образовались наши нын?шнія. Однако же не вс? ученые согласны съ т?мъ, что д?ло шло именно такъ, а не иначе. Н?которые изъ нихъ обратили вниманіе на то, что первыя 4 цифры древнихъ египтянъ, которыми выражаютъ порядковыя числительныя, и, кром? того, цифра 9 сильно напоминаютъ индусскія цифры. Если это такъ, то, значитъ, изобр?тателями цифръ скор?е надо счесть египтянъ, а не индусовъ. На это мы отв?тимъ сл?дующее: подобное предположеніе очень возможно, т?мъ бол?е, что есть въ исторіи намеки на какой-то древн?йшій, ми?ичеекій народъ—кушитовъ, обитателей Э?іопіи и южной части Аравіи, они легко могли быть посредниками между Египтомъ и Индіей и передать цифры отъ египтянъ къ индусамъ.

Второе возраженіе ученыхъ касается того, что истиннымъ посредникомъ въ перенос? индусскихъ цифръ въ Европу можно бы считать греческаго ученаго Пи?агора, жившаго за 500 л?тъ до Р. X. Въ такомъ случа? изобр?теніе цифръ отодвигается очеиь далеко. И это предположеніе опять можно допустить, потому что есть преданіе, что Пи?агоръ много путешествовалъ, заходилъ въ далекіе края Азіи и вывезъ оттуда немало ц?нныхъ научныхъ изобр?теній. Но съ другой стороны, гораздо лучше дать в?ру иному предположенію, именно, что цифры индусовъ заимствовалъ не Пи?агоръ, а его поздн?йшiе ученики, такъ наз. новопи?агорейцы, жившіе въ Александріи, въ Египт?, во II–III ст. по Р. X. Они согласно этому предположенію сообщили цифры арабамъ, властителямъ с?вернаго берега Африки и Испаніи, — маврамъ, а отъ арабовъ могли заимствовать испанцы и итальянцы.

Посл?дняя догадка, касающаяся нашихъ цифръ и, надо сказать, очень неосновательная, хотя и распространенная, заключается въ сл?дующемъ.

Будто бы каждая цифра образовалась изъ столькихъ точекъ или изъ столькихъ черточекъ, сколько въ этомъ числ? единицъ. Если такъ, то цифра 4 состоитъ изъ Ч,

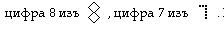
Но этого никакъ не можетъ быть, потому что это чрезвычайная натяжка и одна только игра остроумія. Такимъ путемъ можно всякую цифру привести къ столькимъ черточкамъ или точкамъ, къ сколькимъ угодно.

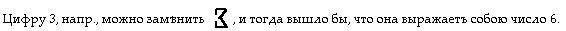
Конечно, единица подходитъ подъ эту гипотезу, и римскія цифры I, II, III, ІІІІ совершенно соотв?тствуютъ ей, но съ индусскими цифрами ничего не сд?лать. Лучшимъ же доказательствомъ несообразности является историческое развитіе цифръ, при которомъ он? много, много разъ м?няли свою форму, д?лались неузнаваемыми, походили одна на другую, и только точное изсл?дованіе историковъ могло разобраться и доказать, какъ изъ одной первоначальной формы вылилась другая окончательная, путемъ многихъ и долгихъ преобразованій. Да и странно было бы думать, что изобр?татели цифръ такіе глубокіе мудрецы, что вложили въ каждую цифру таинственный символъ и образовали цифры изъ соотв?тствующаго числа черточекъ и точекъ.

Какъ сказано уже нами выше, цифры индусовъ были принесены въ Европу въ IX в. по Р. X., но до XIII в. он? распространялись очень слабо.

Причиной этого является недов?ріе, съ которымъ ученые среднихъ в?ковъ встр?тили новинку, хотя бы и полезную. Среднев?ковая школьная ученость (схоластика), правда, не гнушалась св?тскими науками, но въ то же время она слишкомъ высоко ставила латинскій языкъ и римскую цивилизацію.

Западная Европа явилась преемницей и носительнщей научныхъ идей древняго Рима, поэтому-то такъ натурально вышло, что среднев?ковая ари?метика пользовалась исключительно римскимъ абакомъ и римскими цифрами; хотя едва ли римляне оставили другое бол?е неудачное и несовершенное насл?діе, ч?мъ ихъ система ари?метики. Во всякомъ случа? преданіе, инерція превозмогли все, и долго, долго не р?шались ученые среднихъ в?ковъ порвать связь съ абацистами, т.-е. посл?дователями римской ари?метики, и превратиться въ «алгоритмиковъ», поклонниковъ учености арабской. Несм?лыми шагами и тайкомъ, боясь навлечь на себя страшное обвиненіе въ еретичеств?, пробирались сильные умомъ и волею ученые монахи въ Испанію, чтобы тамъ, въ центрахъ мавританской учености, въ Барселон? и Толедо, напитаться открытіями св?жей и новой, чуждой имъ, образованности. Такъ сд?лалъ Гербертъ, св?тлый умъ своего времени, достигшій папскаго престола подъ именемъ Сильвестра II, (? 1003). Крестовые походы, съ ихъ массовымъ передвиженіемъ ц?лыхъ народовъ изъ странъ Европы въ государства Азіи, много сод?йствовали усвоенію науки греческой, арабской, персидской и индусской. Можно сказать, что ари?метика едва ли въ такой степени обязана своимъ развитіемъ другому историческому движенію, въ какой она обязана Крестовымъ походамъ. И зам?чательно, что итальянцы, эти посредники въ сношеніяхъ Европы съ Азіей, особенно чувствовавшіе вліяніе Крестовыхъ походовъ, такъ какъ чрезъ нихъ лилась волна народа въ Азію, явились въ то же время и лучшими математиками. Индусы дали зерно настоящей ари?метики, а итальянцы его выростили.

По роду своихъ занятій прикосновенные къ морской торговл? (недаромъ Христофоръ Колумбъ былъ родомъ итальянецъ), они особенно нуждались въ ари?метик? для своихъ коммерческихъ вычисленiй, прим?няли ее въ банкахъ, конторамъ и т. д. и ув?ков?чили свое имя въ термин? «итальянская бухгалтерія». Индусы любили ари?метику безкорыстно, какъ искусство, и до того ею увлекались, что даже устраивали ц?лые турниры и состязанія въ р?шеніи ари?метическихъ задачъ, итальянцы же приспособили ее прежде всего для ц?лей узкожитейскихъ.

Еще н?сколько словъ объ индусахъ: имъ мы такъ обязаны усовершенствованіемъ ари?метики. Это былъ народъ высококультурный, склонный къ отвлеченному мышленію. Едва ли какой-нибудь другой народъ на ц?ломъ св?т? любилъ настолько жить въ мір? идей, какъ это видимъ у индусовъ. Ихъ чистые созерцатели «факиры» пользуются всемірной изв?стноетью. Об? самыхъ распространенныхъ религіи Азіи, буддизмъ и браманизмъ, получили свое начало въ Индіи. Согласно съ этимъ, математика отличалась у индусовъ идейнымъ, отвлеченнымъ характеромъ и носила алгебраичеекую окраску, въ противоположность грекамъ, поклонникамъ природы и наглядности, которые бол?е любили устремляться на геометрическія построенія. Въ полет? своей математической фантазіи индусы явились изобр?тателями даже не одной, а многихъ ари?метическихъ системъ. Такъ, напр., индусъ Аріабгатта, ученый V в. по Р. X., бралъ 25 согласныхъ буквъ и ими выражалъ вс? числа, начиная съ единицы и оканчивая 25-ю, особыми же буквами обозначалъ онъ и полные десятки до 100; а чтобы обозначить сотни, тысячи и т. д., онъ къ предыдущимъ знакамъ придавалъ гласныя буквы, при чемъ особая гласная обозначала сотни, особая тысячи и т. д. Наирим?ръ, «д» значитъ три, «да»—300, «ди»=30 000, «де» 30 000 000 000. Математики Южной Индіи для каждаго изъ однозначныхъ чиселъ им?ли по н?скольку особыхъ значковъ, — буквъ, также им?лось н?сколько особыхъ знаковъ въ вид? буквъ и для нуля. И вотъ, когда имъ приходилось обозначать разряды какого-нибудь длиннаго числа, она старались вм?сто цифръ подставить буквы такъ, чтобы изъ нихъ составилось какое-нибудь слово, им?ющее смыслъ. Мало того, когда имъ приходил?сь запоминать не одно число, а н?сколько, то они рядъ чиселъ зам?няли ц?лой фразой, которая, опять-таки, им?ла смыслъ. И наконецъ, что всего удивительн?е, при длинномъ ряд? чиселъ, когда изъ нихъ составлялось н?сколько фразъ, индусы ухитрялись сочинять ц?лые стихи и такимъ образомъ запоминать длинныя таблицы; для этого, конечно, нужна большая сноровка и многол?тнія упражненія. И въ наше время среди индусовъ встр?чаются такіе виртуозы, что въ ум? совершаютъ головоломн?йшія вычисленія, не приб?гая къ помощи цифръ. Главный секретъ усп?ха заключается въ этомъ случа? въ томъ, что они при устномъ счет? легко запоминаютъ вс? промежуточные результаты, не теряютъ ихъ и не сбиваются, какъ это непрем?нно случилось бы съ нами; кром? того, конечно, помогаетъ имъ и привычка къ искусственнымъ и сокращеннымъ пріемамъ вычисленія, когда возможно столько упрощеній.