Непрерывныя дроби.

Непрерывныя дроби.

Непрерывныя дроби. Еще у египтянъ встр?чаемъ мы дроби, у которыхъ числитель не ц?лое число; онъ самъ представляетъ изъ себя дробь, напр.

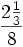
это значитъ 2 вооьмушки и еще сверхъ того треть восьмушки. Так-же и у римлянъ нер?дко ножно было встр?тить

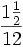
унціи, т. е. 1 дв?надцатую и еще ? дв?надцатой,

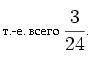
Такимъ образомъ и въ древнемъ мір? идея непрерывныхъ дробей была ясна и доступна: дроби эти основаны на томъ, что числитель можетъ быть не только ц?лое число, но и см?шанное.

Греческій математикъ Архимедъ прим?нялъ непрерывныя дроби къ извлеченію квадратныхъ корней и выражалъ этими дробями приближенныя величины корней. Арабскій ученый Алькальцади (въ XV в. по Р. X.) даетъ н?которые намеки на восходящія непрерывныя дроби; онъ прим?няетъ ихъ къ д?ленію съ остаткомъ и обозначаетъ ими дробное частное. Напр., требуется разд?лить 253 на 280, и такъ какъ 280 разлагается на производителей 5, 7 и 8, то мы сперва д?лимъ 253 на 8, будетъ 31?, потомъ полученное д?лимъ на 7, будетъ

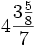
и, наконецъ, д?лимъ на 5, будетъ

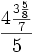
а это, обыкновенно, пр?дставляется такъ:

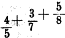
и составляетъ восходящую непрерывную дробь. Нисходящей же дробью была бы такая:

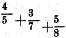
или, если написать ее ясн?е, то

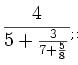
вычислить ее можно такъ:

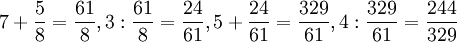
Лордъ Брункеръ, англичанинъ, представилъ (въ 1655 г.) въ вид? непрерывной дроби величину ?/4 = 0, 78539316... (? показываетъ отношеніе длины окружности къ длин? ея діаметра). Гюйгенсъ въ 1682 году далъ подробное объясненіе того, какъ съ помощью непрерывныхъ дробей можно приводить къ легкимъ числамъ трудныя несократимыя дроби. Полную теорію непрерывныхъ дробей далъ Леонгардъ Эйлеръ, н?мецкій ученый 18 в.