Фальшивое правило.

Фальшивое правило.

Существовало и такое правило, и не только существовало, но пользовалось громаднымъ вниманіемъ. По крайней м?р?, у Магницкаго особая 4-я часть его ари?метики была посвящена правиламъ „фальшивымъ или гадательнымъ“, въ то время, какъ въ 1-й части шли д?йствія надъ ц?лыми числами, во 2-й надъ дробями, въ 3-й пом?щено тройное правило и въ 5-й и посл?дней о „прогрессіи и радиксахъ (т. е. корняхъ) квадратныхъ и кубичныхъ". Что же это за фальшивое правило, и почему у него такое странное названіе? Магницкій какъ бы предвидитъ подобный вопросъ и потому объясняетъ успокоительно:

«фальшивая правила, сир?чь не истинная положенія, зане чрезъ два не истинная положенія изобр?таетъ самое оно желаемое истинное число».

 Объяснимъ это правило на общеязв?стной задач? о гусяхъ, кстати она и пом?щена въ ари?метик? Румовскаго (1760 г.), какъ прим?ръ фальшиваго правила. Задача такая:

«лет?ло стадо гусей, на встр?чу имъ летитъ одинъ гусь и говоритъ: здравствуйте, сто гусей, а т? ему отв?чаютъ: н?тъ, насъ не сто гусей, а если бы насъ было еще столько, сколько есть, да еще полъ-столька, да четверть-столька, да еще ты одинъ гусь съ нами, тогда насъ было бы ровно сто гусей. Сколько ихъ было?»

Р?шеніе такое: положимъ, во-первыхъ, что гусей было хоть двадцать; сочтемъ теперь, что составитъ столько, да полъ столько, да четверть столько, да еще одинъ, и выйдетъ всего гусей 20 + 20 + 10 + 5 + 1 = 56; а ихъ надо 100, сл?довательно не достаетъ 44-хъ. Положимъ теперь, во-вторыхъ, что гусей было 24, и сосчитаемъ опять итогъ, выйдетъ 24 + 24 + 12 + 6 + 1=67, не достаетъ до 100 33-хъ. Итакъ, первое предположеніе было 20, недостатокъ 44, второе предположеніе 24, недостатокъ 33. Теперь сл?дуетъ перемножить накрестъ 20 24 и изъ большаго произведенія

20 24

   X

44 33

вычесть меньшее, т.-е. 44 · 24 - 20 · 33 = 1056 - 660= 396 и этотъ остатокъ 396 разд?лить на разницу между обоими недостатками 44 — 33, получится 396 :11 = 36, в?рный отв?тъ задачи. Общее правило выражается такъ: надо принять для вопроса задачи какое-нибудь произвольное значеніе, высчитать тотъ результатъ, который получится, когда подставимъ въ задачу это произвольное число, зат?мъ высчитать погр?шность; точно также берется второе произвольное значеніе и вычисляется второй результатъ и вторая погр?шность; тогда

Способъ фальшиваго правила былъ изв?стенъ индусамъ и арабамъ еще въ IX в. по Р. X., при чемъ выводъ его принадлежитъ, по всей в?роятности, индусамъ. Въ латинскихъ рукописяхъ Парижской библіотеки говорится, что индусское сочиненіе, относящееся къ этому предмету, было переведено въ XII в. на еврейскій языкъ испанскимъ евреемъ Авраамомъ бэнъ-Эзра. Съ еврейскаго языка это сочиненіе было переведено впосл?дствіи на латинскій. У арабскихъ писателей фальшивое правило пользовалось широкимъ распространеніемъ, и объ немъ говорятъ вс? арабскіе математики.

Альхваризми (въ IX в. по Р. X.) даегь сл?дующій прим?ръ: «найти такое число, что если отнять отъ него ? и ? его, то въ остатк? будетъ 8»; положимъ, что число будетъ 12, тогда остатокъ вышелъ бы 5, вм?сто 8, т.-е. на 3 меньше; пусть число 24, тогда остатокъ оказался бы больше настоящаго на 2, теперь въ формул? р?шенія намъ придется сложить 2 произведенія, о которыхъ говорилось выше въ правил?, а не вычесть одно изъ другого, и это потому, что въ задач? одинъ отв?тъ больше настоящаго, а другой меньше его (24.3 +12.2) : (3 + 2) = 19¹/₅. О фальшивомъ правил? много говоритъ также Леонардо Фибонначи, итальянскій математикъ 13 ст. Въ русскихъ математическихъ рукописяхъ XVII в. это правило изв?стно подъ такимъ именемъ: «статья цифирная именуется вымышленая или зат?йчивая. Высокаго остропамятнаго разума и умнаго прилежаніе ея-же н?ціи фальшивою строкою нарекоша, иже ни малымъ ч?мъ погр?шается».

Сущность фальшиваго правила лучше всего объясняется алгебраически. Возьмемъ одно уравненіе первой степени съ однимъ неизв?стнымъ: ax+b = 0. Примемъ x равнымъ произвольному количеству k₁; подставивъ k₁ вм?сто х, пусть мы получимъ во второй части вм?сто нуля т₁, такъ что ak₁ + b = n₁ т.-е. ошибка оказалась во второй части на n₁. Дадимъ иксу другое произвольное значеніе k₂, и пусть вторая часть обратится въ n₂, такъ-что ошибка второй части уравненія будетъ n₂. Теперь мы получимъ такую систему:

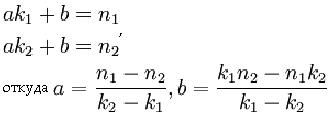
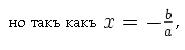
то образуется сл?дующее выраженіе для неизв?стнаго:

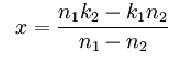
Изъ этой формулы выходитъ: n₁x- n₂x= n₁k₂- n₂k₁, или n₁(x-k₂)=n₂(x-k₁) откуда получается пропорція: n₁: n₂=(х-k₁) : (х-k₂), т. е. ошибки неизв?стныхъ пропорціональны ошибкамъ уравненій. Этой пропорціей и устанавливается связь между фальшивымъ правиломъ и способомъ пропорцій.

Фальшивое правило вводилось во вс? учебники ари?метики до начала 19-го в?ка и считалось необходимой ихъ частью и однимі изъ самыхъ важныхъ отд?ловъ. Оно встр?чается, между прочимъ, въ ари?метик? Безу, переведенной на русскій языкъ В. Загорскимъ въ 1806 году. Въ настоящее время это правило совершенно исключено изъ ари?метическаго курса, и его нигд? найти нельзя. Дв? причинь сод?йствовали его исключенію. Во-первыхъ, выводъ его можетъ быті сд?ланъ только алгебраически и, сл?довательно, въ ари?метик? онъ не можетъ быть объясненъ ученикамъ и требуетъ отъ нихъ прямого заучиванія; во вторыхъ, никакой учебникъ не разграничивалъ, какія задачи можно р?шать фальшивымъ правиломъ, и какихъ нельзя имі р?шать; а, между т?мъ, это существенно важно, потому что, еслі прим?нить правило къ тому, къ чему оно неприм?нимо, то выйдетъ конечно, одно печальное недоразум?ніе. На самомъ д?л? это правило можетъ им?ть силу только для т?хъ задачъ, гд? вся задача сводится къ умноженіямъ и д?леніямъ неизв?стнаго.