Дѣленіе.

Д?леніе.

«Dura cosa e la partita»—звучитъ старинная итальянская поговорка, которая значитъ въ русскомъ перевод?: «трудная вещь—д?леніе». Не даромъ Лука де-Бурго, итальянскій математикъ XVI в?ка, ут?шаетъ начинающихъ учиться юношей и говоритъ, что «кто ум?етъ д?лить, тому все остальное пустяки, потому что все заключается въ д?леніи». И нашъ Магницкій не отстаетъ въ этомъ случа? и тоже, кончивши д?леніе, вздыхаетъ свободно и назидаетъ своихъ «мудролюбивыхъ отроковъ» стихами:

Первую часть докончивше

И вся въ ц?лыхъ изучивше,

Ихъ въ памяти твердо держимъ

И за та вся Бога блажимъ,

Что даде намъ безъ напасти

Зр?ти конецъ первой части.

Трудно д?леніе нашимъ школьникамъ и въ настоящее время. Но неизм?римо, безконечно трудн?е было оно въ старинныя времена и особенно въ начал? среднихъ в?ковъ. Тогда изъ столкновенія римской и арабской учености не усп?ло еще выработаться сколько-нибудь сносной системы, да кром? того, самъ характеръ преподаванія, котораго держались тогда въ монастырскихъ школахъ, былъ сухъ, безсердеченъ, неприноровленъ къ силамъ д?тей и требовалъ отъ нихъ нечелов?ческаго напряженія. Тотъ, кто оказывался въ состояніи понимать д?леніе, признавался чуть не геніемъ и ему давали почетный титулъ «доктора абака», въ род? нашего «доктора математики» или «доктора медицины». Нормальнымъ, зауряднымъ д?тямъ нечего было и мечтать о такомъ трудномъ, мудреномъ д?йствіи, и они скромно ограничивались сложеніемъ и вычитаніемъ, съ придачей таблицы умноженія. Вотъ что значило неум?нье преподавать, отсутствіе понятныхъ учебниковъ и усложненность вычисленій. Вотъ откуда пошло вредное пов?рье, будто для математики надо родиться со спеціальными способностями, и что кто не рожденъ атематикомъ, тотъ не будетъ въ ней усп?вать, несмотря на свое стараніе и на искусство учителя. См?шно теперь слышать, что среднев?ковые педагоги требовали прирожденныхъ способностей для умноженія и д?ленія: в?дь, въ наше время съ ними удачно справляется всякій мальчикъ въ сельской школ? и всякая д?вочка; но курьезъ сохраняется и въ наши дни, когда съ авторитетнымъ видомъ заявляютъ, что для алгебры и геометріи нужны какія-то особыя исключительно математическія способности. Он?, конечно, нужны, но лишь въ такой м?р?, въ какой и для каждаго учебнаго предмета, и виной неусп?ха сл?дуетъ признать, обыкновенно, не отсутствіе способностей, а плохое преподаваніе, особенно вначал?, когда разрабатываются элементы, основы предмета, и когда зарождается расположеніе къ нему. Стоитъ только вм?сто расположенія и пониманія возбудить отвращеніе и непониманіе, и д?ло пропало, при томъ пропало бол?е, ч?мъ въ какомъ бы то ни было другомъ предмет?, потому что въ математик? все посл?дующее вытекаетъ изъ предыдушаго, и если только зародышъ слабъ, то и весь организмъ будетъ хилымъ.

Перейдемъ теперь къ способамъ д?ленія и разберемъ ихъ по порядку.

1) Объясненіе д?ленія начнемъ съ нашего способа и прежде всего зам?тимъ, что имя ему было «золотой» способъ за его удобства и «французскій» за то, что французы предпочитали его бол?е всего. Первые намеки на него мы можемъ вид?ть у Альхваризми, араба, жившаго въ IX в. по Р. X. Въ бол?е ясной форм? онъ встр?чается у индуса Баскары (XII в. по Р. X.). Въ н?мецкой литератур? можно указать на рукопись, найденную въ мюнхенской библіотек? и принадлежащую къ XII в?ку. Въ ней вычисленія располагаются колоннами, при чемъ вверху колоннъ подписано римскими цифрами ихъ значеніе, такъ что въ сущности зд?сь идетъ вычисленіе на абак?. Прим?ръ: 100000:20023 = 4 и ост. 19908.

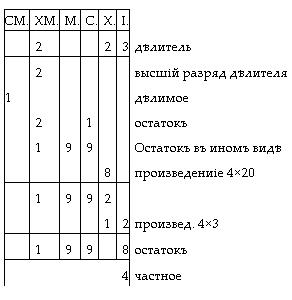
Порядокъ д?йствія, какъ видимъ, такой: подписавши д?лителя и его высшій разрядъ, пом?щаемъ подъ нимъ д?лимое 100000 и задаемся цифрой частнаго; она не будетъ 5, потому что въ д?лител? кром? 20000 есть еще другіе разряды, сл?д. цифра частнаго будетъ 4; такъ какъ 2?4 = 8, а 10 - 8 = 2, то остатокъ посл? высшаго разряда д?лителя, умноженнаго на частное, составитъ 2; дал?е множимъ на частное десятки д?лителя, ихъ всего 2, 2?4=8, но чтобы вычесть 8 дес. изъ 20000, надо сперва 20000 зам?нить черезъ 19900+100 и тогда легко становится отнять 80 отъ 100, остатокъ будетъ 20; наконецъ, 3?4 =12, вычитаемъ 12 изъ 20, получаемъ 8, а всего посл? д?ленія ии?емъ въ остатк? 19908. Частное пишется въ самомъ низу. Вообще во всемъ этомъ прим?р? мы наблюдаемъ ходъ д?йствія такой же, какъ и у насъ, но въ подробностяхъ много особеннаго: не пишется нулей, потому что м?ста цифръ достаточно указываются надписями надъ колоннами; не по нашему расположены д?лимое, д?литель и частное; умноженіе идетъ съ высшихъ разрядовъ; вычитаніе производится постепенно, разрядъ за разрядомъ, какъ только они образуются.

2) Сл?дующій разъ мы встр?чаемся съ этимъ способомъ уже въ XV—XVI в. А какъ же вычисляли въ промежутк? между XII и XVI вв.? Кстати, какъ вычисляли до XII в?ка, в?дь, очевидно, и тогда было д?леніе? Конечно, вычисляли, но только не по нашему пріему, а совс?мъ по другому, непохожему, который развивался и удерживался вплоть до XIX в?ка и въ начал? его исчез, о немъ р?чь будетъ впереди, теперь же приведемъ образецъ нашего д?ленія, который встр?чается у Луки де-Бурго, итальянца. Разд?лить требуется 97535376 на 9876, получится въ частномъ 9876. Расположеніе то же, что и у насъ, только д?литель и частное пишется вверху; а не сбоку.

3) Въ знаменитомъ труд? по ари?метик?, который у арабовъ считается образцовымъ, классическимъ, и который принадлежитъ Бэгаэддину (1547—1622), встр?чается такое расположеніе: (975741: 53= 18410).

Частное пишется въ самомъ верху. Цифры д?лимаго не сносятся внизъ, но вм?сто этого чертятся, для удобства, колонны, чтобы не сбиться въ цифрахъ. Оба разряда д?лителя, 5 дес. и 3 ед., помножаются отд?льно на частное и отд?льно же вычитаются. Д?литель переписывается столько разъ, скодько разрядовъ въ частномъ. Зд?сь повторяется опять то же, что мы вид?ли и въ умноженіи, гд? множитель переписывался н?сколько разъ. Причина опять та же, что и въ умноженіи, и заключается она въ сл?дующемъ. Способъ Бэгаэддина получилъ начало, очевидно, еще тогда, когда вычисленія шли на абак?, покрытомъ пескомъ, и когда, сл?д., легко было д?лителя стереть и его же переписать снова, расположивши снова подъ т?ми разрядамі, которые д?лятся; съ теченіемъ времени абакъ былъ оставленъ, математики стали пользоваться бумагой, а между т?мъ манера переписыванія все еще сохранилась и привела къ большимъ неудобствамъ, къ затрат? лишняго труда, къ потер? времени и м?ста. Вотъ что значитъ инерція, не просв?тленная лучами разума!

4) Апіанъ въ XVI ст. даетъ такое же расположеніе, какое дали бы и мы, но только онъ подписываетъ числа не разрядъ подъ разрядомъ, а просто крайнюю цифру подъ крайней. Разд?лить 97535376 на 9876, получится 9876. Пишется д?лимое, подъ нимъ д?литель, а частное сбоку.     a b c

9 7 5 3 5 3 7 6   ( 9 8 7 6

9 8 7 6

8 8 8 8 4

8 6 5 1 3 a

7 9 0 0 8

7 5 0 5 7 b

6 9 1 3 2

5 9 2 5 6 c

5 9 2 5 6

5) Тарталья, изобр?тательный итальянскій математикъ XVI в., не только учившій по старин?, но и отъ себя предлагавшій много оригинальныхъ и удобныхъ пріемовъ, для большей ясности расчленяетъ д?йствіе на рядъ отд?льныхъ вычисленій, смотря по тому, сколько цифръ въ частномъ.

Вотъ, какъ онъ выполняетъ д?леніе 2596860019 на 38784.

Частное 67019, остатокъ 7807. При этомъ Тарталья говоритъ, что хорошо бы передъ д?леніемъ заготовлять произведенія д?лителя на вс? однозначныя числа; тогда видн?е было бъ, какою цифрою задаваться въ частномъ, да и не нужно составлять отд?льно произведеній д?лителя на цифры частнаго, такъ-какъ они ужъ есть, и останется прямо вычитать.

6) Клавіусъ въ XVII ст. вводитъ нашъ знакъ д?ленія (при помощи угла), но числа при д?леніи располагаетъ не по нашему. Прим?ръ: 1902942 : 2978=639.

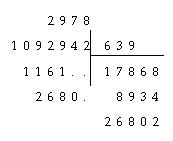
7) Вендлеръ, н?мецкій педагогъ XVII в., употребляетъ почти нашъ пріемъ, съ тою только разницей, что д?литель и частное у него ставятся по об?имъ сторонамъ д?лимаго.

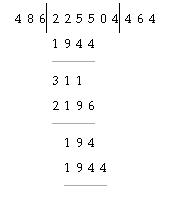
Кром? того, цифры д?лимаго не сносятся, а остаются на своемъ прежнемъ м?ст? вверху.

8) Пешекъ въ XVIII ст. вычисляетъ такъ же, какъ и Вендлеръ. Пешекъ даетъ нашему способу названіе французскаго.

9) Баргь въ XVIII ст. пишетъ д?лителя подъ д?лимымъ при всякомъ частномъ д?леніи, сл?д. столько разъ, сколько разрядовъ въ частномъ. 66734 : 325= 205 ¹⁰⁹/₃₂₅

10) Въ русскихъ математическихъ рукописяхъ XVII стол?тія встр?чаются, какъ и сл?довало ожидать, т? же самые пріемы, какіе выработала Западная Европа. Они перешли къ намъ черезъ Польшу, такъ какъ именно польская ученость давала пищу русской образованности XVII в?ка. Чаще всего въ это время встр?чается способъ Апіана (см. выше, 4). У Магницкаго, стр. К а оборот? представлено д?леніе въ такомъ вид?.

Зд?сь д?лимое 5175 пом?щено во второй строк?, частное справа, д?литель 15 переписывается трижды (въ третьей и пятой строкахъ), четвертая и пятая строка отведены частнымъ произведеніямъ, а верхняя—остатку отъ вычитанія. Изъ этого видно, что цифры расположены довольно несистематично и неудобно, такъ что сбиться въ нихъ очень легко. Но, по правилу, «изъ двухъ золъ выбирай менынее», Магницкій очень доволенъ этимъ способомъ и одобряетъ его въ сл?дующихъ выраженіяхъ: «Мнози убо д?лятъ перечни сицевымъ образомъ: егда д?лителемъ емлютъ, изъ числъ д?лимаго, и написавши за чертою, умножаютъ имъ весь д?литель и, подписавши вычитаніемъ, вычитаютъ изъ д?лимаго. И намъ видится, сицевымъ образомъ есть удобн?йше, но т?мъ иже слаб?йшеее разум?ніе и тщаніе имутъ: зане не толикаго есть домышленія, и остроты». Дал?е у Магницкаго идетъ способъ, цохожій на Барта (см. выше, 9), и способъ Вендлера (выше, 7). Вліяніе Вендлера вполн? зам?тно въ ари?метик? Василія Адодурова (1740 г), Румовскаго (1760 г.), Кузнецова (1760 г.). У Загорскаго (1806 г.) является нашъ нормальный способъ во всей чистот?.