Цифры различныхъ народовъ

We use cookies. Read the Privacy and Cookie Policy

Цифры различныхъ народовъ

Немного есть наукъ, которыя свое начало вели бы съ такихъ древнихъ временъ, какъ ари?метика. И среди этихъ немногихъ своихъ спутницъ ари?метика является наукой самой отвлеченной. Но если ужъ теперь, несмотря на то, что цивилизація и общее развитіе значительно проникли въ массу народа, всякое отвлеченное мышленіе все же очитается ч?мъ-то сухимъ и труднымъ, то т?мъ бол?е во времена давно прошедшія отвлеченное знаніе нуждалось обязательно во вн?шнемъ проявленіи. Цифры и служатъ такимъ проявленіемъ. Он? всеобщи и такъ же древни, какъ древни крайніе зачатки ари?метики. Такъ, цифры у египтянъ мы видимъ за 2200 л?тъ до Р. Хр. въ папирус? Ринда, у халдеевъ за 2300 л?тъ до Р. X. въ табличкахъ Сенкере и у китайцевъ за 2637 л?тъ до Р. X. въ «Кіу-чанг?», составленномъ ученымъ авторомъ Тзинъ-кіу-чау. Много есть разныхъ сортовъ цифръ; они отличаются другъ отъ друга и происхожденіемъ, и начертаніемъ, въ зависимости отъ того, когда они получили начало и у какого именно народа.

Нав?рное, читатель, вамъ приходилось не разъ зам?чать, что малые ребята съ особенной охотою рисуютъ дома, людей, животныхъ, т.-е. все то, что прямо предъ глазами, и лишь потомъ, впосл?дствіи они берутся за условные рисунки, т.-е. значки, планы и чертежи. Такъ точно и народы древности предпочитали им?ть цифры въ вид? рисунковъ т?хъ предметовъ, которые у нихъ передъ глазами. Особенно зам?тна эта оклонность у древнихъ египтянъ, хотя и у другихъ народовъ мы можемъ указать подобные сл?ды. Это письмо носитъ названіе гіероглифичеекаго; напр., чертежъ шеста или кола обозначалъ собою единицу; десятокъ означался фигурою 2-хъ соединенныхъ рукъ, такъ какъ на 2 рукахъ бываетъ 10 пальцевъ; символомъ сотни считался свернутый пальмовый листъ, такъ какъ съ его развитіемъ выходитъ изъ него много листовъ, можетъ быть до 100; тысяча рисовалась въ вид? цв?тка лотоса, который знаменовалъ собой обиліе; цифрой, которая обозначала 10000, было изображеніе лягушки, такъ какъ лягушки при разливахъ Нила являлись въ неисчислимомъ количеетв?, многими тысячами. Картиной милліона была фигура изумленнаго челов?ка.

Такими гіероглифами пользовался Египетъ для выраженія вс?хъ чиселъ. Подобная система была и у халдеевъ. У римлянъ цифра V напоминаетъ своей формой кисть руки. Но, очевидно, писать при помощи рисунковъ крайне медлительно и неудобно, въ особенности же потому, что каждый изъ рисунковъ необходимо было повторять по многу разъ. Такъ, чтобы выразить число хоть 30270, египтянинъ 3 раза рисовалъ лягушку, 2 раза листъ и 7 разъ сложенныя руки. Гіероглифы надо было упростить, снабдить ихъ легкой формой и прим?нимостыо къ письму. Ви?сто фигуръ стали чертить лишь облики, н?что въ род? условныхъ знаковъ. Такъ получились цифры. Вром? того, писать одинъ и тотъ же знакъ по многу разъ невыгодно и долго, поэтому египтяне придумали для чиселъ 2, 3, 4, 9 свои особые значки, которые давали имъ возиожность изб?жать длиннаго и утомительнаго повторенія цифры 1. Что же касается 5, 6, 7, 8, то эти цифры у египтянъ были составлены изъ 2, 3, 4.

Сл?ды письма гіероглифами, какъ сказано уже выше, мы видимъ у халдеевъ. Но и они оставили эту систему и выработали вм?сто нея новую, очень посл?довательную и простую, такъ называемое клинообразное письмо. Чтобъ обозначить единицу, халдеи рисовали вертикальную черту съ заостреннымъ нижнимъ краемъ и толстымъ расщепленнымъ верхнимъ. Десятокъ означался такою же чертой, но только въ положеніи горизонтальномъ и съ острымъ краемъ, обращеннымъ вл?во. Для выраженія н?сколькихъ единицъ халдеи повторяли столько разъ знакъ единицы, еколько ихъ содержалось въ данномъ чиел?. Такъ, напр., чтобы выразить 7 единицъ, они писали 7 разъ знакъ единицы. Такимъ же образомъ они писали и десятки. Сотню оии обозначали помощью 2 чертъ, горизонтальной вм?ст? съ вертикальной. Для чиселъ, состоящихъ изъ полныхъ сотенъ порядокъ видоизм?нялся: именно, халдеи брали знакъ сотни и при немъ писали столько разъ единицу, сколько сотенъ въ заданномъ числ?. Для тысячи халдеи не им?ли особенной цифры, и они обозначали тысячу, какъ десять согенъ. И такъ, халдейская система цифръ, равно какъ и египетская, основаны на непосредственной наглядности, и отъ нея уже он? переходятъ къ условнымъ знакамъ.

Еще такого же происхожденія мы видимъ цифры у китайцевъ. Въ первоначальной своей форм? он? напоминаютъ картины т?хъ шнуровъ и косточекъ, которые употреблялись при наглядномъ счет?. Впосл?дствіи цифры китайцевъ сильно изм?нились и приняли н?сколько видовъ. У нихъ есть разныя цифры: древне — китайскія, торговыя, научныя и для правительственныхъ актовъ. Цифры древне-китайскія очень фигурны и замысловаты и весьма возможно, что он? явились изм?неніемъ начальныхъ гіероглифовъ; он? писались на листкахъ не въ строчку, а вертикальнымъ столбикомъ, располагаясь сверху внизъ. Наоборотъ, цифры торговыя писались горизонтальными строками и шли сл?ва направо; при этомъ числа разлагались на разряды, такъ что разрядъ писался за разрядомъ. Чтобы прочесть число, китайцы прямо говорили т? слова, какія соотв?тствуютъ написанному ряду цифръ; согласно ихъ произношенію, тридцать = три десять, тринадцать = десять три, девяносто = девять десять.

Итакъ, у египтянъ, халдеевъ и китайцевъ мы видимъ дифры древн?йшаго происхожденія, которыя напоминаютъ собою гіероглифы, или картины т?хъ предметовъ, которые стоятъ въ связи съ даннымъ числомъ. Другимъ основнымъ корнемъ, давшимъ начало цифрамъ, являются числительныя имена. Это уже цифры бол?е поздн?йшія, такъ какъ для ихъ изображенія необходимо было развиться алфавиту, грамотности, потребности въ письм? и достаточному искусству письменнаго изложенія. У н?которыхъ народовъ, какъ, напр., у финикіянъ, нер?дко выписывались числителъныя имена сполна, черезъ посредство буквъ и словъ: финикіяне прямо записывали числа, согласно ихъ произношенію, словами, а не пользовались особыми значками — цифрами. Иногда такой же способъ прим?няли и греки, но особенно его любили арабы. Существуетъ ц?лый учебникъ по ари?метик? араба Алькархи (въ 11 ст. по Р. X.), гд? н?тъ ни одной цифры, и вс? вычисленія, даже довольно сложныя, выполнены словесно.

Но очевидно, что подобное выписываніе числительныхъ именъ крайне неудобно и утомительно. Въ силу этого, числительныя имена стали подвергаться сокращенію. и цифрами стали считаться начальныя буквы числительныхъ именъ. Прим?ровъ этому мы видимъ много у грековъ и у римлянъ, у индусовъ и у арабовъ (въ ихъ поздн?йшихъ цифрахъ). Греческія слова «пять» (?????), десять (????), тысяча (??????), десять тысячъ (??????) начинались съ буквъ ?, ?, ?, ?, поэтому именно такія буквы являлись у грековъ знаками для чиселъ 5, 10, 1000, 10000, такъ что, согласно первоначальному греческому обозначенію, число пять им?ло цифру ?, десять ?, тысяча ?, и, наконецъ, десять тысячъ ?. Подобный счетъ описанъ византійскимъ грамматистомъ Геродіаномъ, и этотъ сортъ греческихъ цифръ называется геродіановыми цифрами. Подобной же системой воспользовались и арабы, когда они, наконецъ, поняли, что полностью писать числительныя имена довольно затруднительно, они тоже стали писать только начальныя буквы числительныхъ именъ.

И наконецъ, посл?дней стадіей развитія, хотя и близкой къ нашимъ временамъ, но вовсе неудобной, и потому оставленной, надо признать такой порядокъ, когда зам?ной цифръ служили буквы въ посл?довательности алфавита. Такъ напр., греческій алфавитъ содержитъ по порядку буквы: ?, ?, ?, ?, ?, въ виду этого и числа обозначались: единица — ?, два—?, три—?, четыре — ?, пять—?. Греки придумали обозначать такимъ образомъ приблизительно со временъ Рождества Христова, а до этого они приб?гали къ геродіановымъ цифрамъ. Всл?дствіе этого буква ? стала обозначать уже не десять, какъ начальная буква греческаго слова «????», что значитъ десять, но она стала выражать четыре, какъ 4-я буква алфавита. Какое же удобство въ этихъ поздн?йшихъ цифрахъ сравнителыш съ т?ми, которыя указалъ Геродіанъ? Ари?метически н?тъ совершенно никакого, и пользы отъ зам?ны однихъ значковъ другими не представляется никакой; виной такой зам?ны явились, в?роятно, переписчики, которымъ слишкомъ трудно было помнить буквы вразбросъ и въ безпорядк?: они и предпочли расположить ихъ въ порядк?. Подобную же систему мы видимъ у славянъ и у евреевъ. Несомн?нно, она заимствована отъ грековъ.

Повторимъ вкратц? еще разъ, что цифры вс?хъ народовъ и временъ распред?ляются на три разряда: 1) цифры, получившія начало отъ гіероглифовъ и обратившіяся въ условные знаки; 2) цифры, образовавшіяся изъ буквъ алфавита и представляющія собой начальныя буквы числительныхъ именъ, и 3) цифры въ порядк? буквъ алфавита. Вторая категорія цифръ тоже изм?нилась, подобно первой, въ н?которыхъ случаяхъ до неузнаваемости, такъ что изъ буквъ образовались условные знаки.

Теперь мы сообщимъ н?которыя подробности о цифрахъ отд?льныхъ народовъ[3]

Египтяне. Они были образованнымъ народомъ уже за 4000 л?тъ до Р. X. Періодическіе разливы Нила рано побудили ихъ заниматься землем?ріемъ и ари?метикой, такъ какъ каждую весну приходилось имъ снова разм?рять, расчислять и д?лить поля, затянутыя иломъ

могучей р?ки. Въ 1872 году въ тайникахъ одной изъ многочисленныхъ египетскихъ цирамидъ нашли свертокъ пергамента, такъ наз. папирусъ «Риндъ», въ которомъ разобрали рукопись ари?иетическаго содержанія. Авторъ ея н?кто египтянинъ Амесъ, жившій во времена фараона Аменемы (2221–2179 г. до Р. X.). Изъ рукописи можно усмотр?ть, что автору доступны были довольно сложныя задачи замысловатаго характера не только въ ц?лыхъ числахъ, но и съ дробями.

У египтянъ было три системы письма: а) гіероглифическая, о которой упомянуто выше, в) гіератическая, или письмо жрецовъ, и с) простонародная. Письмо гіератическое является нич?мъ инымъ, какъ упрощеніемъ гіероглифовъ, и въ этомъ смысл? его можно считать нормальнымъ переходомъ къ цифрамъ. Пользуясь знаками единицы, десятка, сотни, тысячи, египтяне ихъ повторяли столько разъ, сколько хот?ли обозначить единицъ, десятковъ и т. д.; но выше 1000 въ гіератическомъ письм? они вводили умноженіе: такъ, чтобы обозначить 10000, они писали рядомъ 10 и 1000. Письмо простонародное преподавалось въ школахъ и прим?нялось въ обиходной жизни, въ торговл?, письмахъ, въ гражданскихъ документахъ. Оно им?ло, въ свою очередь, не мало разныхъ видовъ; одинъ изъ нихъ нами показанъ въ приложеніи 3-мъ. Когда египтяне им?ли д?ло съ большими числами, то высшіе разряды они писали сл?ва, а низшіе направо, т.-е. точь въ точь, какъ мы.

Финикіяне. Они были моряками и купцами древняго міра. Имъ приписывается изобр?теніе алфавита и усп?шное развитіе ари?метическихъ знаній. Алфавитъ финикіянъ состоялъ изъ 22 буквъ, похожихъ на египетскіе гіероглифы. Служили-ль эти буквы также и для обозначенія чиселъ, на это н?тъ никакихъ указаній. Напротивъ того, несомн?нно, что финикіяне или писали сполна слова, выражающія числа, или же пользовались особыми, спеціальными цифрами. Изъ этихъ цифръ и составлялись обозначенія чиселъ, при чемъ рядомъ стоящія цифры иногда являлись множителями другъ друга, иногда же он? подлежали сложенію. Числа отъ 1 до 9 обозначались соотв?тственнымъ количествомъ вертикальныхъ черточекъ. Горизонтальная черта или уголъ, обращенный отверстіемъ внизъ, обозначали число 10. Нал?во (не не направо, какъ написали бы мы) отъ этого знака раcполагали 1, 2, 3 и т. д. вертикальныхъ черты, для обозначенія чиселъ отъ 11 до 19. Такъ, напр. «||||—» обозначало четырнадцать. Чтобы обозначить два десятка, финикіяне писали 2 параллельныхъ черты, которыя лежали горизонтально. Для 100 былъ тоже особый знакъ, именно I<I.

Изъ Тира и Сидона, древнихъ финикійскихъ городовъ, расположенныхъ на берегу Средизеинаго моря, центровъ тогдашней торговли, процв?тавшихъ съ XIV до VIII в?ка до Р. X., распространилось счетное искусство по финикійскимъ колоніямъ, которыя были разс?яны по берегу С?верной Африки и южнымъ полуостровамъ Европы.

Халдеи, см?шавшіеся съ вавилонянами и подчинившіе ихъ себ?, жили на южномъ теченіи р?къ Тигра и Евфрата. Это сос?ди и счастливые противники іудеевъ ветхаго зав?та. Культура ихъ принадлежитъ къ древн?йшимъ: она началась бол?е ч?мъ за 3000 л?тъ до Р. X., и пришла въ упадокъ за 500 л?тъ до Р. X. Халдеи употребляли для письма н?что въ род? грифелей, съ расщепленными концами, поэтому-то мы и видимъ у нихъ такъ назыв. клинообразное письмо. Цифры халдеевъ приведены выше и представлены подробно въ приложеніи 4-мъ, въ конц? книги. Ихъ можно хорошо установить, благодаря счастливой находк?, которую удалось сд?лать въ развалинахъ древняго знаменитаго города Ниневіи. Тамъ подъ грудой мусора, пыли и пепла археологи открыли ц?лую сохранившуюся залу, по нашему сказать, библіотеку, устроенную по приказанію царя Сарданапала за 7 стол?тій до Р. X. Это была публичная библіотека. Вотъ еще когда и вотъ еще въ какихъ странахъ открывались публичныя библіотеки! Но книгъ въ ней не было, а были ц?лые ряды тонкихъ глиняныхъ плитокъ, обожженныхъ и прочныхъ, расписанныхъ разными красками: это нарисованы буквы, фразы и ц?лыя сочиненія. Есть среди нихъ и сочиненія ари?метическаго содержанія.

Обширная торговля, вм?ст? съ развитіемъ ремеслъ, заставила халдеевъ заняться практическими вычисленіями; этимъ любознательный народъ не удовольствовался и перешелъ къ теоретическимъ вопросамъ ари?метики. Мало того, халдеи стали искать какихъ-то скрытыхъ, таинственныхъ свойствъ чиселъ, стали гадать на числахъ, волхвовать, предсказывать; цифрамъ придавался смыслъ символическій, и ими угадывали будущее. Какъ это бываетъ везд? и всегда, легков?рные люди создали халдеямъ репутацію искусныхъ гадальщиковъ. Въ 139 г. до Р. X. они были изгнаны изъ Рима за волшебство. Но слава ихъ и вліяніе былн зам?тны еще въ средиіе в?ка въ Западной Европ?, такъ что имъ приписываютъ особыя кабалистическія цифры, употреблявшіяся въ астрологіи (см. 7-е приложеніе).

Греки. Древн?йшія цифры грековъ мы указали выше. Поздн?йшими цифрами, прим?рно за 100 л?тъ до Р. X., стали служить буквы алфавита въ ихъ нормальномъ порядк?. Единицы, десятки и сотни обозначаются по этой систем? такъ: 1=?, 2=?, 3=?, 4=?, 5=?, 6=?, 7=?, 8=?, 9=?, 10=?, 20=?, 30=?, 40=?, 50=?, 60=?, 70=?, 80=?, 90=?, 100=?, 200=?, 300=?, 400=?, 500=?, 600=?, 700=?, 800=?, 900=??. Тутъ, какъ видно, всего цифръ 27, а буквъ у грековъ въ алфавит? им?ется только 24; поэтому пришлось добавить къ нимъ еще 3 буквы старинныхъ, давно уже вышедшихъ изъ практики, такъ наз. v?v, koppa и sampi, для обозначенія 6, 90 и 900.

Чтобы отличить число отъ слова, греки проводили обыкновенно надъ цифрами черту, такъ, напр., —?—?[4]=15,—?—?—?=122. Для обозначенія тысячъ они пользовались опять 9-ю первыми знаками, но подъ ними проводили маленькую вертикальную черту, наприм?ръ, |?=1000, |?=2000, |?=3000, |—?—?—?—?=1575, |—?—?—?=5380, |—?—?—?—?= 9843, |—?—?—?—?=3654.

Десятокъ тысячъ составляетъ новую употребительную едииицу счета — миріаду. Греки любили пользоваться миріадами и прии?няли ихъ съ такою же охотой, cъ какой мы прим?няемъ тысячи и милліоны; можно сказать, что въ греческомъ счисленіи классъ состоялъ изъ 4 разрядовъ, а не изъ 3-хъ, какъ въ нашемъ, такъ что при выговариваніи большихъ чиселъ они прежде всего указывали миріады, а посл? нихъ и тысячи и остальные вс? разряды. Знакъ миріады былъ М или М?. Дв? миріады обозначались черезъ ?M.

Миріада миріадъ, по нашему сто милліоновъ, обозначалась черезъ М?. Миріада въ куб?, иначе сказать трилліонъ, писалась М?. Отд?льаыя же миріады разд?лялись точками, поэтому: М?.?|M?.??|M?.|???=5601052800000. Какъ видно, цифры зд?сь располагаются отъ л?вой руки къ правой, но это было не всегда, и такой порядокъ не считался обязательнымъ: можно было писать отъ правой руки къ л?вой; въ Сициліи и Малой Азіи даже и выговариваніе чиселъ происходило отъ низшаго разряда къ высшему, такъ что сперва произносились единицы, зат?мъ десятки, сотни, тысячи и высшіе разряды.

Буквы — цифры гораздо мен?е удобны, ч?мъ выше упомянутые знаки Геродіана. Внося немало сбивчивости при письм?, он?, кром? того, м?шаютъ производству д?йствій, такъ какъ при нихъ надо въ отд?льности учиться, какъ вычислять съ простыми единицами, въ отд?льности съ десятками и съ прочими разрядами: н?тъ аналогіи и мало сходства въ вычисленіяхъ съ отд?льными разрядами.

Евреи. Они употребляли вм?сто цифръ буквы алфавита. Очевидно, они это сд?лали подъ вліяніемъ гречесжихъ ученыхъ, жившихъ въ Александріи, въ Египт?. Точно сказать нельзя, когда именно евреи перешли къ такой систем? цифръ; но, в?роятно, это случилось незадолго до Р. X., по крайней м?р?, на еврейскихъ монетахъ такія цифры встр?чаются не ран?е 137 г. до Р. X.

Числа отъ 1 до 9 выражались у евреевъ первыми 9-ю буквами алфавита, круглые десятки (20, 30…. 90) девятью сл?дующими буквами, зат?мъ круглыя сотни— 100, 200, 300, 400 выражались четырьмя остальными, потому что въ еврейскомъ алфавит? было всего навсего 22 буквы. И вотъ для остальныхъ круглыхъ сотенъ буквъ недоставало. Первоначально этотъ недостатокъ пополнялся т?мъ, что вм?сто 500 писали 400+100, 600=400+200 и т. д. Потомъ догадались отс?чь концы у 5 слишкомъ длинныхъ буквъ (Капхъ, Мемъ, Нунъ, Пхе, Тцаде) и этими концами начали обозначать остальныя сотни. Еврейскія цифры см. въ приложеніи 8-мъ, въ конц? книги.

Тысячи обозначались опять при помощи 9 первыхъ буквъ, но только надъ ними ставились точки, чтобъ не см?шать съ простыми единицами. Чтобъ отличить числа отъ словъ, употребляли въ первомъ случа? особый знакъ. Цифры писались отъ правой руки къ л?вой, въ порядк? уменьшающейся величины значеній; сл?довательно, разряды низшіе писались вл?во, а не вправо, какъ пишутся у насъ. Впрочемъ, у вс?хъ народовъ такъ наз. семитическаго корня, т.-е. евреевъ, вавилонянъ, арабовъ, финикіянъ, эфіоповъ, ассиріянъ, письмо шло противоположно нашему, т.-е. отъ правой руки къ л?вой.

Сирийцы. Ихъ цивилизація относится къ гораздо бол?е поздн?йшимъ временамъ, ч?мъ финикійская, халдейская, египетская и т. д. Ихъ можно бы назвать въ н?которомъ род? преемниками финикіянъ. По крайней м?р?, въ III в. по Р. X. мы встр?чаемъ у сирійцевъ цифры, которыя очень похожи на т?, какія были въ Финикіи за много л?тъ до Р. X. Поздн?е эти цифры быди отброшены, и, начиная приблизительно съ VII в. по Р. X., сирійская литература содержитъ буквы алфавита вм?сто цифръ. Зд?сь мы находимъ то же самое, что въ Греціи и у евреевъ. Сирійскій алфавитъ, какъ и еврейскій, содержитъ 22 буквы. Для выраженія простыхъ единицъ, круглыхъ десятковъ и сотенъ отъ 100 до 500, буквъ алфавита было достаточно, какъ видимъ мы и у евреевъ. 500, 600 и дал?е до 10001 сирійцы означали при помощи сложенія, такъ что 500=400+100, 600=400+200 и т. д. Круглыя тысячи они писали какъ простыя единицы, только внизу нал?во приписывали запятую. Значеніе десятковъ тысячъ давалось единицамъ и десяткамъ при помощи маленькой горизонтальной черточки, которою подчеркивались цифры. Значеніе милліона давалось 2-мя запятыми.

Славяне. Составитель славянскаго алфавита, св. Кириллъ, заимствовалъ систему цифръ ц?ликомъ у грековъ. Какъ греки пользовались буквами своего алфавита, такъ и для славянъ была составленаі таблица, схожая даже до мелочей съ греческою. Напр., почему 2 обозначаетея по славянски черезъ в?ди, а не черезъ буки? Потому что въ греческомъ язык? н?тъ отд?льныхъ звуковъ «б» и «в», а есть для нихъ общая буква «вита» или «бета». Почему ?ита обозначаетъ девять, хотя ей м?сто въ самомъ конц? алфавита? Потому что въ греческомъ язык? ей соотв?тствуетъ буква ?, которая и стоитъ зд?сь на своемъ м?ст?, а не въ конц? алфавита. Червь, обозначающій 90, поставленъ вм?сто коппы, такъ какъ по-гречески н?тъ звука «ч» совс?мъ, а по-славянски н?тъ коппы. Вотъ рядъ славянскихъ цифръ:

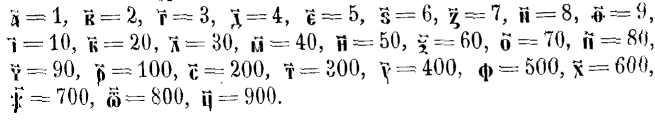
Тысячи обозначаются т?ми же буквами, какими и единицы, но съ добавленіемъ значка, который ставится нал?во отъ цифръ, выражающихъ количество тысячъ. Вообще славянская система—полн?йшая копія греческой: такъ же берутся буквы алфавита, похоже обозначаются тысячи, и даже есть наклонность къ счету миріадами, т. е. десятками тысячъ. Впрочемъ, большія числа въ старинныхъ рукописныхъ славянскихъ сборникахъ встр?чаются не очень часто. Ниже, въ прилож. 9-мъ, приводимъ мы обозначенія большихъ количествъ: тьмы, легіона, леодра, врановъ. Эти изображенія встр?чаются въ старинныхъ рукописяхъ грамматическихъ, но не ари?метическихъ, такъ какъ въ ари?метическихъ рукописяхъ 16–17 стол?тія предпочитаютъ пользоваться цифрами обыкновенными, которымъ мы даемъ названіе арабскихъ.

Римляне. Ихъ система цифръ не принадлежитъ къ числу удобныхъ и разработанныхъ. Римляне были слабы въ ари?метик?, и даже до того слабы, что имъ никакъ не удалось освободиться отъ пережитковъ старой пятеричной системы счета, и только они одни остались при счет? пятками въ то время, какъ вс? другіе народы, начавши, быть-можетъ, тоже со счета пятками, сум?ли выработать чистый счетъ десятками. Цифры у римлянъ см?шанныя: одн? изъ нихъ обязаны своимъ происхожденіемъ наглядности, а другія представляютъ собой буквы.

Римскія цифры таковы: I=1, V=5, X==10, L=50, C=100, D=500, М=1000. Изъ этихъ семи знаковъ легко можно составить обозначенія вс?хъ чиселъ. Тысяча иногда обозначалась не черезъ М, а черезъ (I), т. е. она обозначалась чертой среди 2 скобокъ. Согласно этому, и десятокъ тысячъ им?лъ знакъ такой: ((I)), сто тысячъ (((I))), для милліоновъ брали ?.

При помощи раздваиванія 3-хъ посл?днихъ знаковъ можно образовать 3 новыхъ цифры: І))=5000, І)))=50000, O | = 500000. Отсюда ясно видно, какъ получилось D для пятисотъ; это ничто иное, какъ тысяча (I), разд?ленная пополамъ, правая часть взята, а л?вая откинута.

Значенія отд?льныхъ знаковъ при письм? чаще всего складывались, напр., III=3, ХIII=13, MDCCCLXVI=1866. Но если высшій знакъ стоялъ прав?е низшаго, то это выражало отниманіе, такъ, напр., IX=9, XC=90. Вычитать обыкновенно можно было не больше одного знака, а прикладывать—не больше 3-хъ однородныхъ. Кром? того, прежде ч?мъ писать число, его разлагали на единицы, десятки, сотни и т. д., и чтобы написать хотя бы 990, писали сперва 900, зат?мъ уже 90, т.-е. CMXC, а не отнимали прямо отъ тысячи десятокъ. Бывали, впрочемъ, изр?дка и исключенія: IIX=8, вм?сто VIII; VIIII=9, вм?сто IX; посл?дняя фигура (VIIII) была особенно употребительна на памятникахъ и плитахъ, потому что римляне любили точность, а между т?мъ если подойти съ другой стороны, то IX покажется не 9-ю, а 11-ю (XI).

Только у однихъ римлянъ и видимъ мы отниманіе низшаго знака отъ высшаго, ни у какого другого народа н?тъ подобнаго обыкновенія; если и ставился у другихъ народовъ низшій знакъ перед высшимъ, то онъ указывалъ обыкновенно на повтореніе, а не на отниманіе. Даже и въ произношеніи у римлянъ было вычитаніе, особенно же если вычиталось 2 или 1, такъ, напр., вм?сто восемнадцати они говорили двадцать безъ двухъ. Только въ случа? тысячъ низшій знакъ показывалъ умноженіе и, напр., десять тысячъ можно было писать черезъ X M=10?1000, а сто тысячъ черезъ CM; въ посл?днемъ случа? являлась полная возможность см?шать 100000 съ 900, потому что не видно было, надо ли 1000 взять сто разъ или же отнять 100 отъ 1000.

Точно такъ же писали иногда MM, и въ этомъ случа? опять не видно было, сколько тысячъ обозначено зтой формулой: или это дв? тысячи (М+М), или тысяча тысячъ (М?М), и то и другое чтеніе им?етъ свои основанія и можетъ считаться правильныиъ приходилось догадываться по смыслу, какое именно число надо подразум?вать въ каждомъ отд?льномъ случа?. Чтобы изб?жать сомн?ній и ошибокъ, римляне стали употреблять еще новый пріемъ по которому тысячи обозначались горизонтальной линіей вверху; этимъ пріемомъ 1000 пишется ?, 100000=—С,[5] 1000000=—M, равнымъ образомъ —C—C=200000, —C—L—X=160000.

Знакъ |?| над цыфрами придавалъ имъ значеніе сотенъ тысячъ, такъ наприм?ръ |—X—V—I—I | = 1700000, |—M|= 1000.100000 = 100 000 000. Знаменітый ученый и естествоиспытатель Плинiй (въ I в?к? по Р. X.) ввелъ знакъ для тысячъ точку, сл?довательно L.D=50500. Встр?чаемъ и еще обозначеніе: Vm.=5000.

Теперь мы видимъ и ясно можемъ уб?диться. насколько весь порядокъ нумераціи у римлянъ былъ сбивчивъ, непосл?дователенъ и могь представить много поводовъ къ толкованіямъ въ ту и другую сторону. В?рн?е всего мы отъ римлянъ заимствовали обыкновеніе, чтобъ сумму денегъ въ разныхъ векселяхъ, распискахъ и т. д. писать не только цифрами, но и словами. Для римлянъ это было очень важно и настоятельно необходимо, потому что вс? эти черточки при цифрахъ легко можно стереть, продолжить и пополнить. Исторія передаетъ намъ случай, когда изъ-за неясности написаннаго ряда цифръ произошелъ большой споръ относительно зав?щаннаго насл?дства. Гальба получилъ отъ Ливіи Августы по зав?щанію 50 милліоновъ сестерцій (приблиз. 5 милліоновъ рублей), но Тиверій, главный насл?дникъ, сум?лъ доказать, что подъ этими цифрами надо разум?ть только 500 000 сестерцій; ему это удалось т?мъ легче, чтс сумма денегъ не была написана словами.

При выговариваніи большихъ чиселъ у римлянъ не было въ распоряженіи другихъ словъ, кром? тысячи. Поэтому 1000 000 000 они читали такъ: тысячью тысяча разъ по тысяч?.

Относительно происхожденія римскихъ цифръ существуетъ много различныхъ мн?ній и догадокъ. Н?которые полагагюъ, что начало этимъ цифрамъ дано буквами стариннаго алфавита. Другіе объясняютъ такъ: первыя три цифры I, II и III само собой понятны: он? произошли отъ счета линій; цифра V образовалась изъ картины руки, т.-е. пяти пальцевъ, потому что, если бы очертить кисть руки съ раздвинутыми пальцами, то и получилась бы фигура, напоминающая цифру V; цифра десять своею формой косого креста разлагается на 2 пятка X приложенныхъ другъ къ другу острыми концами; «С», которое обозначаетъ сто, является первой буквой числительнаго «Centum», что значитъ сто; M—тысяча, это начальная буква латинскаго слова «Mille» (тысяча). О томъ, какъ получился знакъ пятисотъ D, нами уже сказано выше. Такъ же можно объяснить и знакъ пятидесяти L, именно сто [, а 50 = ?, т.-е. знакъ ста раздвоенъ на дв? половины, изъ которыхъ нижняя взята, а верхняя половина отброшена.