Задача трех тел

Задача трех тел

Пуанкаре первым из ведущих математиков понял, что все наши уравнения по сути своей предельны. Он ввел понятие нелинейности: малые события могут вести к серьезным последствиям; эта идея стала популярной, возможно, даже слишком популярной, в виде «теории хаоса». Почему эта популярность вредна? Потому что нелинейность, по мысли Пуанкаре, — это серьезный довод, ограничивающий пределы предсказуемости, а вовсе не призыв использовать математические методы для расширения зоны прогнозов. Математика и сама может с легкостью продемонстрировать нам, что ее возможности не безграничны.

Были в истории открытия нелинейности и свои сюрпризы (а как же иначе?). Началось все с того, что Пуанкаре принял участие в конкурсе, который математик Густав Миттаг-Леффлер приурочил к шестидесятилетию шведского короля Оскара. Мемуар Пуанкаре о стабильности Солнечной системы I получил высшую на тот момент научную награду (это было? счастливое время, когда еще не существовало на свете Нобелевской премии). И вдруг досадная неожиданность: научный редактор, проверявший статью перед публикацией, обнаружил ошибку в вычислениях. Однако выяснилось, что, если ее поправить, выводы получаются прямо противоположными: система непредсказуема (если использовать математический термин — неинтегрируема). Публикацию благоразумно задержали, статья — исправленная — вышла через год.

Аргументация Пуанкаре была проста: при предсказании будущего динамику рассматриваемого процесса нужно моделировать со все возрастающей точностью, так как предел погрешности очень быстро возрастает. Проблема в том, что необходимая точность невозможна: «размытость» вашего прогноза внезапно достигает апогея — наступает момент, когда от вас требуется бесконечно точное знание прошлого. Пуанкаре продемонстрировал это на очень наглядном примере, известном как задача трех тел. Если в системе, устроенной по принципу Солнечной, имеется только две планеты и на их орбиты более ничто не влияет, то вы без всяких хлопот сможете предсказывать поведение этих планет. Но поместите между ними третье небесное тело, пусть даже малюсенькую комету. Сначала движение этого третьего тела никак не сказывается на двух других телах, а потом вдруг раз — и его воздействие уподобляется мощному взрыву. Малейшие перемены в расположении этого крохотного тела в конце концов предопределят будущее планет-левиафанов.

И чем мудреней механика, тем труднее предсказывать такие «взрывы». Наш мир, к сожалению, намного сложнее, чем задача трех тел: в нем не три объекта, а гораздо больше. Тут мы имеем дело с тем, что нынче называется динамической системой, а мир, как мы видим, — система весьма динамическая.

Вообразите, что будущее — это ствол с ветвями, каждая из которых образует развилки с множеством ответвлений. Чтобы представить, как пасует наша интуиция перед этими множащимися нелинейными эффектами, вспомните знаменитую притчу о шахматной доске. Изобретатель шахмат попросил следующую награду: одно зернышко риса на первую клетку, два на вторую, четыре на третью, потом восемь, шестнадцать и так далее, каждый раз (всего шестьдесят четыре раза) удваивая количество. Правитель сразу согласился исполнить столь ничтожную просьбу, но вскоре понял, что его перехитрили. Обещанное количество риса превысило бы все мыслимые запасы!

Эта мультипликативная сложность, требующая для прогнозирования все большей и большей точности исходных данных, может быть проиллюстрирована следующим простым упражнением: предсказанием передвижения бильярдного шара по столу. (Я использую в этом примере расчеты, выполненные математиком Майклом Берри.) Если вы знаете все основные параметры покоящегося шара, можете рассчитать сопротивление поверхности стола (это элементарно) и силу удара, то довольно просто определите, что случится при первом столкновении. Предсказать последствия второго удара будет труднее, но тоже возможно: придется лишь уточнить уже измеренные параметры. Но чем дальше, тем хуже: для корректного расчета девятого удара нужно учесть гравитационное воздействие тела, находящегося возле стола (по скромным прикидкам Берри, в этом теле менее 70 килограммов). А для расчета пятьдесят шестого удара в ваших вычислениях должны будут присутствовать все элементарные частицы Вселенной. Электрон на краю Вселенной, отделенный от нас 10 миллиардами световых лет, может оказать значимый эффект на результат. Помните о дополнительной трудности: нужно также принять во внимание все прогнозы относительно местоположения этих переменных в будущем. Чтобы предсказать движение бильярдного шара по столу, нужно знать динамику всей Вселенной, каждого атома! Мы можем легко предсказать траектории крупных объектов, скажем, планет (хотя на довольно малом отрезке времени), но для объектов поменьше их уже так просто не рассчитаешь — а этих объектов неизмеримо больше, чем крупных.

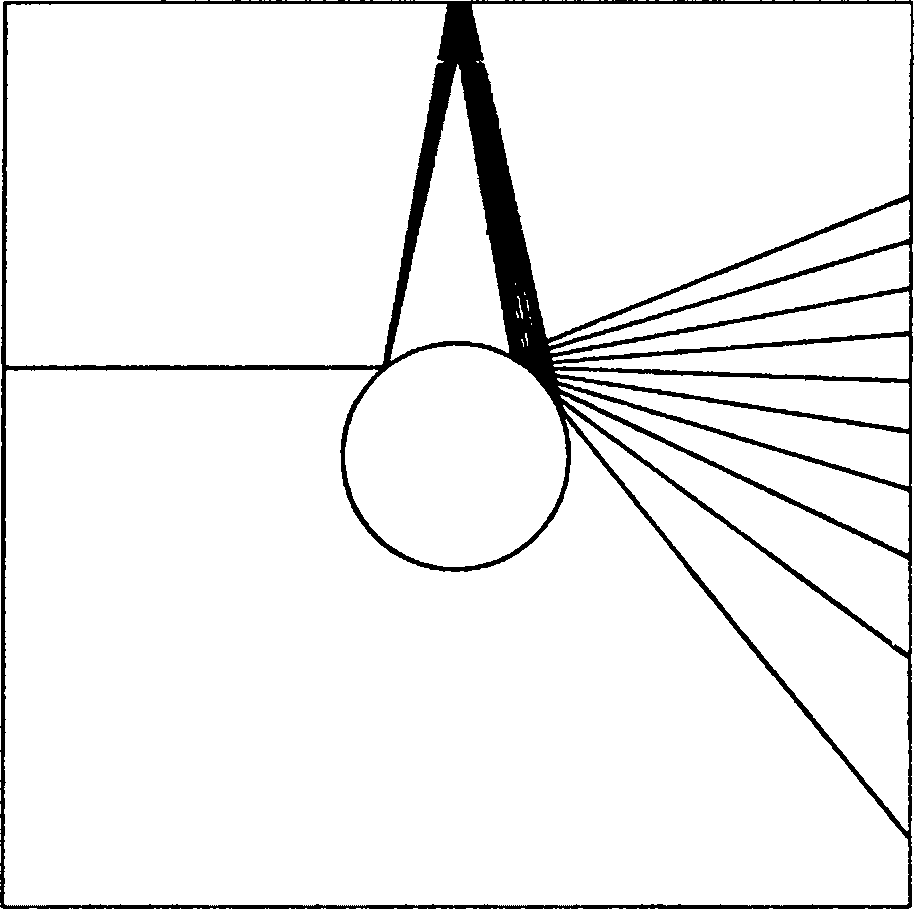
Дэвид Коуэн, прочитавший эту книгу в черновом варианте, нарисовал изящную картинку рассеивания. Мы видим, как уже при втором рикошете расхождения в начальных условиях могут приводить к совершенно разным последствиям. С каждым соприкосновением будут множиться и возрастать отклонения от начального угла падения. Это вызывает усиливающийся со временем эффект: ошибка растет несоразмерно быстро.

Заметьте, что в примере с бильярдными шарами мы имели в виду некий абстрактный мир, простой и понятный, без социальных безумств, которые творятся иногда совершенно произвольно. У бильярдных шаров нет разума. В примере также не учитываются квантовый эффект и эффект относительности. Мы не использовали и понятие (к которому часто обращаются шарлатаны) «принцип неопределенности». Нас не волнует, что на субатомном уровне точность измерений крайне ограниченна. Мы занимаемся исключительно самими бильярдными шарами!

При наличии динамической системы, где помимо одного-единственного шара имеются и другие объекты, где траектории до некоторой степени зависят друг от друга, возможность предсказывать будущее не просто уменьшается — она становится предельно ограниченной. Пуанкаре предложил работать только с качественными, а не с количественными величинами: обсуждать некоторые свойства систем, но не просчитывать их. Можно точно мыслить, но нельзя использовать числа. Пуанкаре даже придумал для этого специальный метод — анализ in situ[51], воспринятый топологией. Предсказание и прогнозирование — дело куда более сложное, чем обычно считают, но, чтобы понять это, нужно знать математику. А чтобы принять это, нужно и понимание и мужество.

В 1960-х метеоролог Эдвард Лоренц из Массачусетского технологического института самостоятельно повторил открытие Пуанкаре — опять же случайно. Он работал над компьютерной программой погоды, моделируя ее динамику на несколько дней вперед. Как-то он попытался воспроизвести ту же модель, введя те же, как ему казалось, исходные параметры, но получил совершенно иные результаты. Сначала он решил, что дело в компьютерном сбое или ошибке вычисления. Первые компьютеры были чудовищно громоздкими, работали медленно, не то что нынешние, поэтому их пользователи всегда искали способ их «поторопить». Лоренц быстро сообразил, что столь значительные расхождения в результатах произошли из-за того, что ради упрощения задачи он несколько округлил исходные параметры. Это явление было названо «эффектом бабочки»: взмах крыльев индийской бабочки может два года спустя вызвать ураган в Нью-Йорке. Открытие Лоренца пробудило интерес к «теории хаоса».

Разумеется, исследователи обнаружили, что открытие Лоренца было предвосхищено трудами не только Пуанкаре, но и прозорливого интуитивиста Жака Адамара, который размышлял о тех же проблемах примерно в 1898 году, а потом прожил еще почти семь десятилетий и умер в возрасте 98 лет[52].

Данный текст является ознакомительным фрагментом.